No hard maths, not yet
There arenít any mathematicians at Rolloworks, just enthusiasts. We think the maths of the Tubie is interesting and ask any reader who can supply some serious analysis of the puzzle to get in touch, and we will incorporate it.
Permutations of pattern
On a 6-wheel Tubie, regardless of pin layout, there are 6^5=7776 different arrangements of the patterns on the cells. This is nothing compared to many puzzles, so why isn't it easier? Because very often as you make a step towards your target something gets in the way and moves you away from it at the same time. Tubies with more wheels will become harder very noticeably. The 10-wheel version on the Bowling playscreen has 10 million different arrangements, and is challenging to say the least.
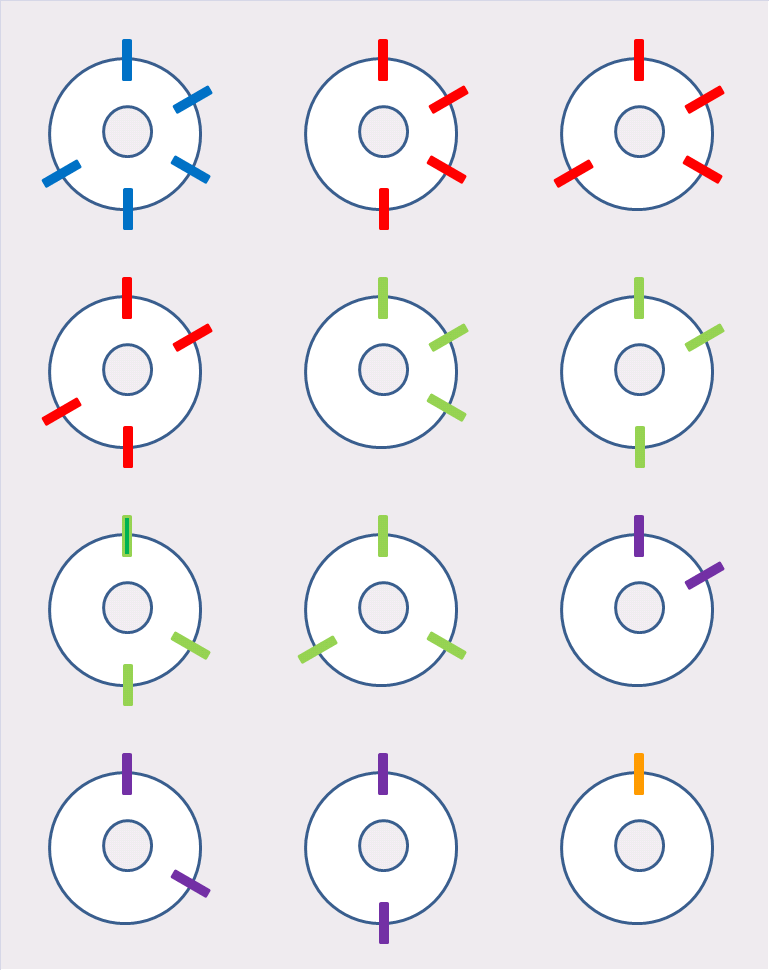
Combinations of pins
On the 6-wheel version, there are many possible arrangements of pins. The picture above shows the distinct pin arrangements possible on a wheel with six cells, excluding 0 pins and 6 pins. Any of these can be turned against any other by coming in with the finbar at the right point. With 12 wheels available, the number of ways to combine five wheels is 12x11x10x9x8 / 5! = 792 possible combinations.
(Note that the number of permutations, or distinct arrangements, would be higher by a factor of 120 (5!) but all Tubies are put together in such a way that there is never any confusion about whether two units are functionally the same, just differently ordered. The order is: Reference Wheel then Most Pins down to Fewest Pins, where wheels with an equal number of pins are ordered from Most Clustered to Least Clustered, which is the order shown above reading each wheel clockwise from 12 o'clock.)
One-way functions
Pretentious, moi? Maybe, but the connections with cryptography and modular arithmetic are easily spotted. In most puzzles it is easy to undo a move. Even in the cube, so long as you can remember what you've done, you can reverse your way back to the start. With the Tubie you can't, because pins frequently adopt new neighbours and cannot be disentangled. We're not sure what this means beyond complicating the analysis, but perhaps someone can help.
Inaccessible positions
Since all wheels can be turned relative to all others, it seemed obvious that any line-up of cells would be reachable by judicious use of the finbar. However it turns out that not all positions can be reached after all. For example, it is impossible to get a line of National Speed Limit signs on this Driving model.
About 3% of all positions occupy little islands of inaccessibility on the standard 12-pin layout. No matter how you approach the target position, the pins are located so that you are deflected around it. Another way to consider it is by imagining you have reached the target position, and then make a single move away. None of these moves can be reversed. Try it here. We would welcome further insight into this interesting area.
Solutions
Two things turned the Tubie from a neat mechanism into a serious puzzle. The first was the introduction of the stationary wheel, which made it easy to select a target and gauge your progress towards it. The second was the idea of the Start position (improbably called En-Ra-Ha in honour of Mike Leigh) where the red pins are lined up. This gave the puzzle a competitive element and a basis for analysing positions and move sequences.
On the standard 12-pin model, using perfect play, any reachable position can be found in eight moves or less. This is the only pin layout for which all moves have been catalogued, and for which solutions can be obtained on the Solutions page. Other layouts will be fully analysed in the coming months. The assumption is that the more pins there are, the longer the maximum journey will be, and perhaps the more inaccessible positions there are, but that all has yet to be seen. Again, unless somebody knows otherwise. Please write in.
Meanwhile, most of the playscreens are looking for best scores. We want you to drive these down to the minimum, or even prove what the minimum has to be - over to you.
